
Zadanie Podróż (pod)
Pomóż nam usprawnić bazę zadań!
Travel
Memory limit: 32 MB
Let us consider a diagram describing a net of municipal transportation, for example a bus-net, tram-net or underground-net etc. Vertices of the diagram (numbered 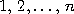 ), correspond to stations, edges
), correspond to stations, edges 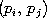 , (where
, (where 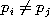 ) denote that there is a direct connections from the station
) denote that there is a direct connections from the station 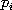 to the station
to the station 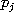 (
(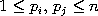 ). Transportation lines are numbered
). Transportation lines are numbered 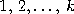 . The transportation line no.
. The transportation line no.  is defined as a series of stations
is defined as a series of stations 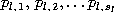 , on which vehicles of the line no.
, on which vehicles of the line no. 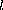 stop, and durations
stop, and durations 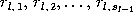 of traveling between stations -
of traveling between stations -  is the time necessary to get from the station
is the time necessary to get from the station 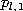 to the station
to the station 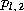 , or vice versa (i.e. from the station
, or vice versa (i.e. from the station 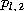 to the station
to the station 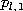 );
); 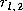 is the time necessary to get from the station
is the time necessary to get from the station 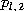 to
to 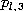 , etc. All the stations of a line are different (i.e.
, etc. All the stations of a line are different (i.e. 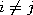 implies
implies 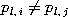 ). In the transportation line no.
). In the transportation line no. 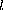 vehicles run with certain frequency
vehicles run with certain frequency 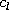 , where
, where 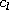 is a number from the set
is a number from the set 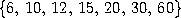 . The vehicles in the transportation line no.
. The vehicles in the transportation line no. 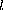 start from the station
start from the station 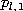 at each hour of the day and night,
at each hour of the day and night, 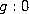 , (
, (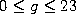 ), and than according to the frequency of the line i.e. at
), and than according to the frequency of the line i.e. at  etc. (
etc. (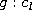 means
means 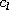 minutes after hour
minutes after hour 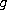 ). Vehicles of the line
). Vehicles of the line 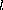 run in two directions: from the station
run in two directions: from the station 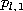 to
to 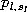 , and from the station
, and from the station 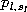 to
to 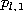 . The hours of departure of the vehicles of the transportation line no.
. The hours of departure of the vehicles of the transportation line no. 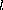 from the station
from the station 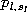 are the same as from the station
are the same as from the station 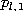 .
.
In such a transportation net we want to make a trip from the start station  to the finish station
to the finish station 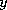 . We assume that the trip is possible and will take no longer than 24 hours. During the trip one can change transportation lines as many times as he/she wants to. Say, the time of a change is equal to 0, however, while changing the line we have to take under consideration the time of waiting for the vehicle that we want to get into. Our purpose is to get from the start station
. We assume that the trip is possible and will take no longer than 24 hours. During the trip one can change transportation lines as many times as he/she wants to. Say, the time of a change is equal to 0, however, while changing the line we have to take under consideration the time of waiting for the vehicle that we want to get into. Our purpose is to get from the start station  , to the finish station
, to the finish station 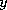 , as quick as it is possible.
, as quick as it is possible.
Example
On the picture below you can see a scheme of the transportation net with 6 stations and two lines: no. 1 and no. 2. Vehicles of the line no. 1 go between stations 1, 3, 4 and 6, vehicles of the line no. 2 go between stations 2, 4, 3 and 5. The frequencies with which the vehicles run are equal to 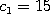 and
and 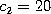 respectively. The durations of travel between stations are written next to the edges of the net; they are given indices 1 and 2 for particular lines.
respectively. The durations of travel between stations are written next to the edges of the net; they are given indices 1 and 2 for particular lines.
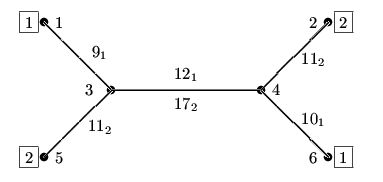
Let us assume, that at 23:30 we stay on the station no. 5 and we want to get to the station no. 6. It is necessary to wait 10 minutes and then (at 23:40) one can leave using line no. 2. There are two options of our trip. The first option is to get to the station no. 3 at 23:51, wait 3 minutes, change to the line no. 1 at 23:54 and get to the station 6 at 0:16 (the next day). The second option is to take the line no. 2 and get to the station no. 4 at 0:8 a.m., we wait 13 minutes and at 0:21 a.m. we take the vehicle of the line no. 1 and we get to the station no. 6 at 0:31. Thus the earliest time we can get to the station no. 6 is at 0:16.
Task
Write a program which:
- reads from the standard input the description of the transportation net, transportation lines, number of the start station
 , number of the finish station
, number of the finish station 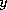 , the hour and minute of the beginning of the trip -
, the hour and minute of the beginning of the trip - 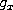 and
and 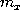 respectively,
respectively, - finds the shortest time of the trip from the start station
 to the finish station
to the finish station 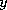 ,
, - writes to the standard output the earliest possible time of getting to the finish station
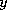 -
- 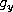 and
and 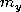 (hour and minute respectively).
(hour and minute respectively).
Input
In the first line of the standard input there are written six integers, separated by single spaces:
- the number of stations
 (
(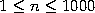 ),
), - the number of lines
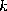 (
(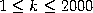 ),
), - the number of the start station
 (
(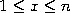 ),
), - the number of the finish station
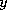 (
(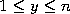 ),
), - the hour of the beginning of the trip
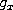 (
(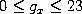 ),
), - the minute of the beginning of the trip
 (
(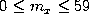 ).
).
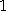 to
to  , the transportation lines from
, the transportation lines from 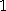 to
to 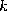 . In the following
. In the following 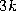 lines the transportation lines are described - the description of each of them takes three consecutive lines.
lines the transportation lines are described - the description of each of them takes three consecutive lines.
- In the first line describing the transportation line no.
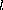 there are written two integers, separated by a single space:
there are written two integers, separated by a single space: 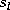 , the number of stations (
, the number of stations (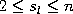 ), and
), and 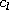 - the frequency with which the vehicles run (
- the frequency with which the vehicles run (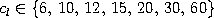 ).
). - In the second line describing the transportation line no.
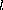 there are
there are 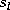 different integers, separated by single spaces:
different integers, separated by single spaces: 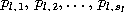 - the numbers of consecutive stations on the transportation line no.
- the numbers of consecutive stations on the transportation line no. 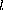 (
(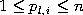 , for
, for 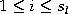 ).
). - In the third line describing the transportation line no.
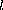 there are written
there are written 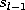 integers separated by single spaces:
integers separated by single spaces: 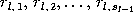 - the times (in minutes) necessary to go between the consecutive stations of this transportation line (
- the times (in minutes) necessary to go between the consecutive stations of this transportation line (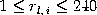 , for
, for 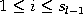 ).
).
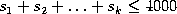 ).
).
Output
Your program should write in the only line of the standard output two integers, separated by a single space: the hour of the earliest possible arrival to the finish station 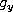 (
(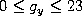 ) and the minute of the earliest possible arrival to the finish station
) and the minute of the earliest possible arrival to the finish station 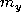 (
(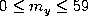 ).
).
Example
For the input data:
6 2 5 6 23 30 4 15 1 3 4 6 9 12 10 4 20 5 3 4 2 11 17 11
the correct result is:
0 16
Task author: Zbigniew Czech.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English